8  Asreml-R

First we need to load the asreml library:

library(asreml)

Loading required package: Matrix

Online License checked out Tue Oct  8 11:38:02 2024

Loading ASReml-R version 4.2

8.0.1 Estimating repeatability

With repeated measures on individuals it is often of interest to see how repeatable a trait is. We can estimate the repeatability of a trait as the proportion of phenotypic variance \(V_P\) explained by individual variance \(V_{ind}\); \(R = V_{ind}/V_P = V_{ind}/(V_{ind}+V_R)\).

modelv <- asreml(
  fixed = laydate ~ 1,
  random = ~animal,
  residual = ~ idv(units),
  data = gryphonRM,
  na.action = na.method(x = "omit", y = "omit")
)

ASReml Version 4.2 08/10/2024 11:38:03
          LogLik        Sigma2     DF     wall
 1     -10182.83           1.0   1606   11:38:03
 2     -8266.097           1.0   1606   11:38:03
 3     -6145.012           1.0   1606   11:38:03
 4     -4651.572           1.0   1606   11:38:03
 5     -3819.309           1.0   1606   11:38:03
 6     -3554.215           1.0   1606   11:38:03
 7     -3501.557           1.0   1606   11:38:03
 8     -3497.576           1.0   1606   11:38:03
 9     -3497.536           1.0   1606   11:38:03
10     -3497.536           1.0   1606   11:38:03

plot(modelv)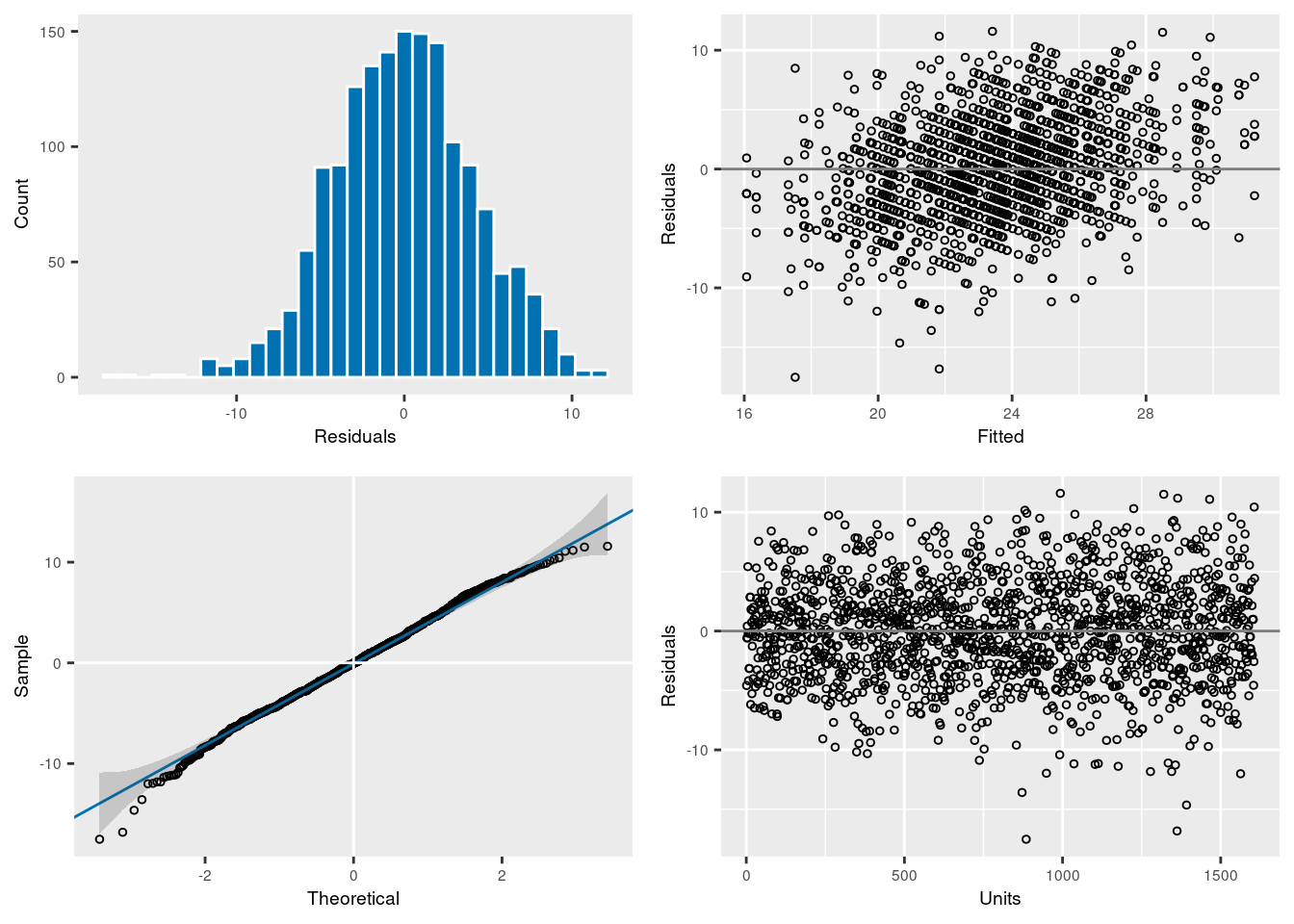

The model assumption seems correct, so we can look at the different estimates. Note that since we want to estimate the amount of variance explained by individual identity (rather than by additive genetic effects), we fit animal as a normal random effect and we don’t associate it with the pedigree. Here, we also ask the model to remove any NA in laydate.

This model partitions the phenotypic variance in laydate as follows:

summary(modelv)$varcomp

            component std.error   z.ratio bound %ch
animal       11.08634 1.1794319  9.399728     P   0
units!units  21.29643 0.8896196 23.938798     P   0
units!R       1.00000        NA        NA     F   0

Between-individual (or among-individual) variance is given by the animal component, while the residual component (units!units) represents within-individual variance. Here then the repeatability of the trait can be determined by hand as 0.34 (i.e., as 11.086/(11.086 + 21.296)).

Mean lay date might change with age, so we could ask what the repeatability of lay date is after conditioning on age. This would be done by adding age into the model as a fixed effect.

modelw <- asreml(
  fixed = laydate ~ age,
  random = ~animal,
  residual = ~ idv(units),
  data = gryphonRM,
  na.action = na.method(x = "omit", y = "omit")
)

ASReml Version 4.2 08/10/2024 11:38:04
          LogLik        Sigma2     DF     wall
 1     -8402.968           1.0   1602   11:38:04
 2     -6912.361           1.0   1602   11:38:04
 3     -5274.379           1.0   1602   11:38:04
 4     -4143.634           1.0   1602   11:38:04
 5     -3541.895           1.0   1602   11:38:04
 6     -3372.909           1.0   1602   11:38:04
 7     -3347.670           1.0   1602   11:38:04
 8     -3346.655           1.0   1602   11:38:04
 9     -3346.652           1.0   1602   11:38:04

summary(modelw)$varcomp

            component std.error  z.ratio bound %ch
animal       12.28982  1.156115 10.63027     P   0
units!units  16.37989  0.686619 23.85586     P   0
units!R       1.00000        NA       NA     F   0

The repeatability of lay date, after accounting for age effects, is now estimated as 0.43 (i.e., as 12.29/(12.29 + 16.38)). So, just as we saw when estimating \(h^2\) in Tutorial 1, the inclusion of fixed effects will alter the estimated effect size if we determine total phenotypic variance as the sum of the variance components. Thus, proper interpretation is vital.

summary(modelw, coef = TRUE)$coef.fixed

             solution std error   z.ratio
(Intercept) 20.305073 0.2899515 70.029214
age_2        0.000000        NA        NA
age_3        2.577777 0.3355253  7.682811
age_4        4.247276 0.3309028 12.835418
age_5        6.094490 0.3375537 18.054872
age_6        3.132675 0.3371074  9.292811

wald.asreml(modelw, ssType = "conditional", denDF = "numeric")

ASReml Version 4.2 08/10/2024 11:38:04
          LogLik        Sigma2     DF     wall
 1     -3346.652           1.0   1602   11:38:04
 2     -3346.652           1.0   1602   11:38:04

$Wald
[0;34m
Wald tests for fixed effects.[0m
[0;34mResponse: laydate[0m

            Df  denDF   F.inc   F.con Margin Pr
(Intercept)  1  460.2 14880.0 14880.0         0
age          4 1225.3    88.7    88.7      A  0

$stratumVariances
                   df Variance  animal units!units
animal       463.8399 56.46460 3.26162           1
units!units 1138.1601 16.37989 0.00000           1

Here age is modeled as a 5-level factor (specified using the function as.factor() at the beginning of the analysis). We could equally have fitted it as a continuous variable, in which case, given potential for a late life decline, we would probably also include a quadratic term. In addition, using age as continuous variable can help in saving some degree of freedom in the analysis.

8.0.2 Partitioning additive and permanent environment effects

Generally we expect that the repeatability will set the upper limit for heritability since among individual variation can be decomposed in the additive genetic variation and non additive genetic variation. In other word, the additive genetic variation is a subcomponent of the difference between individuals. Non-additive contributions to fixed among-individual differences are normally referred to as permanent environment effects. If a trait has repeated measures then it is necessary to model permanent environment effects in an animal model to prevent upward bias in \(V_A\).

To illustrate it, we first fit the animal model:

gryphonped <- read.csv("data/gryphonped.csv")
gryphonped$id <- as.factor(gryphonped$id)
gryphonped$father <- as.factor(gryphonped$father)
gryphonped$mother <- as.factor(gryphonped$mother)

ainv <- ainverse(gryphonped)

modelx <- asreml(
  fixed = laydate ~ age,
  random = ~ vm(animal, ainv),
  residual = ~ idv(units),
  data = gryphonRM,
  na.action = na.method(x = "omit", y = "omit")
)

ASReml Version 4.2 08/10/2024 11:38:05
          LogLik        Sigma2     DF     wall
 1     -8751.390           1.0   1602   11:38:05
 2     -7169.205           1.0   1602   11:38:05
 3     -5427.604           1.0   1602   11:38:05
 4     -4219.598           1.0   1602   11:38:05
 5     -3569.815           1.0   1602   11:38:05
 6     -3382.341           1.0   1602   11:38:05
 7     -3352.867           1.0   1602   11:38:05
 8     -3351.565           1.0   1602   11:38:05
 9     -3351.560           1.0   1602   11:38:05

Variance components are almost unchanged if we compare the previous model:

summary(modelx)$varcomp

                 component std.error   z.ratio bound %ch
vm(animal, ainv)  13.91784  1.443968  9.638607     P   0
units!units       16.84008  0.707365 23.806768     P   0
units!R            1.00000        NA        NA     F   0

summary(modelw)$varcomp

            component std.error  z.ratio bound %ch
animal       12.28982  1.156115 10.63027     P   0
units!units  16.37989  0.686619 23.85586     P   0
units!R       1.00000        NA       NA     F   0

This suggests that most of the among-individual variance is – rightly or wrongly – being partitioned as \(V_A\) here. To instead to obtain an unbiased estimate of \(V_A\), we need to partition for both additive genetic and non-genetic sources of individual variation. We do it by fitting animal twice, once with a pedigree, and once without a pedigree (using ide()). Here, the command ide allow to create a second effect using a similar variable.

modely <- asreml(
  fixed = laydate ~ age,
  random = ~ vm(animal, ainv) + ide(animal),
  residual = ~ idv(units),
  data = gryphonRM,
  na.action = na.method(x = "omit", y = "omit")
)

ASReml Version 4.2 08/10/2024 11:38:05
          LogLik        Sigma2     DF     wall
 1     -7731.394           1.0   1602   11:38:06
 2     -6426.548           1.0   1602   11:38:06
 3     -4997.252           1.0   1602   11:38:06
 4     -4018.486           1.0   1602   11:38:06
 5     -3504.988           1.0   1602   11:38:06
 6     -3363.160           1.0   1602   11:38:06
 7     -3341.611           1.0   1602   11:38:06
 8     -3340.682           1.0   1602   11:38:06
 9     -3340.679           1.0   1602   11:38:06

summary(modely)$varcomp

                 component std.error   z.ratio bound %ch
vm(animal, ainv)  4.876101 1.8087709  2.695809     P   0
ide(animal)       7.400983 1.7280113  4.282948     P   0
units!units      16.380188 0.6866189 23.856300     P   0
units!R           1.000000        NA        NA     F   0

The estimate of \(V_A\) is now much lower since the additive and permanent environment effects are being properly separated. We can estimate \(h^2\) and the repeatability from this model:

vpredict(modely, h2 ~ V1 / (V1 + V2 + V3))

    Estimate         SE
h2 0.1701523 0.06073974

vpredict(modely, repeatability ~ (V1 + V2) / (V1 + V2 + V3))

               Estimate         SE
repeatability 0.4284108 0.02741602

8.0.3 Adding additional effects and testing significance

Models of repeated measures can be extended to include other fixed or random effects. For example try including year of measurement (year) and birth year (byear) as random effects.

modelz <- asreml(
  fixed = laydate ~ age,
  random = ~ vm(animal, ainv) + ide(animal) +
    year + byear,
  residual = ~ idv(units),
  data = gryphonRM,
  na.action = na.method(x = "omit", y = "omit")
)

ASReml Version 4.2 08/10/2024 11:38:06
          LogLik        Sigma2     DF     wall
 1     -4650.748           1.0   1602   11:38:06
 2     -4088.264           1.0   1602   11:38:06
 3     -3494.147           1.0   1602   11:38:06
 4     -3127.161           1.0   1602   11:38:06  (  1 restrained)
 5     -2976.449           1.0   1602   11:38:06  (  1 restrained)
 6     -2955.785           1.0   1602   11:38:06  (  1 restrained)
 7     -2955.097           1.0   1602   11:38:06  (  1 restrained)
 8     -2955.095           1.0   1602   11:38:06  (  1 restrained)
 9     -2955.095           1.0   1602   11:38:06

summary(modelz)$varcomp

                    component std.error   z.ratio bound %ch
byear            1.650876e-07        NA        NA     B  NA
year             7.938576e+00 1.9344619  4.103765     P   0
vm(animal, ainv) 4.815136e+00 1.6682351  2.886365     P   0
ide(animal)      8.433325e+00 1.5495778  5.442337     P   0
units!units      7.795560e+00 0.3324411 23.449443     P   0
units!R          1.000000e+00        NA        NA     F   0

This model will return additional variance components corresponding to variation in lay dates between years of measurement and between birth cohorts of females. \(V_{byear}\) is very low and B appeared which tell us that the model had fixed the variance as a boundary. If you compare this model to a reduced model with byear excluded the log-likelihood remains unchanged.

modelz_2 <- asreml(
  fixed = laydate ~ age,
  random = ~ vm(animal, ainv) + ide(animal) +
    year,
  residual = ~ idv(units),
  data = gryphonRM,
  na.action = na.method(x = "omit", y = "omit")
)

ASReml Version 4.2 08/10/2024 11:38:06
          LogLik        Sigma2     DF     wall
 1     -4665.606           1.0   1602   11:38:06
 2     -4097.928           1.0   1602   11:38:06
 3     -3498.611           1.0   1602   11:38:06
 4     -3128.789           1.0   1602   11:38:06
 5     -2976.883           1.0   1602   11:38:06
 6     -2955.806           1.0   1602   11:38:06
 7     -2955.096           1.0   1602   11:38:06
 8     -2955.095           1.0   1602   11:38:06

summary(modelz_2)$varcomp

                 component std.error   z.ratio bound %ch
year              7.938576 1.9344829  4.103720     P   0
vm(animal, ainv)  4.815137 1.6682366  2.886364     P   0
ide(animal)       8.433324 1.5495828  5.442319     P   0
units!units       7.795560 0.3324384 23.449637     P   0
units!R           1.000000        NA        NA     F   0

modelz$loglik

[1] -2955.095

modelz_2$loglik

[1] -2955.095

1 - pchisq(2 * (modelz_2$loglik - modelz$loglik), 1)

[1] 0.9990453

year effects could alternatively be included as fixed effects (try it!). This will reduce \(V_R\) and increase the estimates of heritability and repeatability, which must now be interpreted as proportions of phenotypic variance after conditioning on both age and year of measurement effects.

modelz_3 <- asreml(
  fixed = laydate ~ age + byear,
  random = ~ vm(animal, ainv) + ide(animal) +
    year,
  residual = ~ idv(units),
  data = gryphonRM,
  na.action = na.method(x = "omit", y = "omit")
)

ASReml Version 4.2 08/10/2024 11:38:06
          LogLik        Sigma2     DF     wall
 1     -4623.985           1.0   1569   11:38:07
 2     -4063.535           1.0   1569   11:38:07
 3     -3471.618           1.0   1569   11:38:07
 4     -3105.972           1.0   1569   11:38:07
 5     -2955.436           1.0   1569   11:38:07
 6     -2934.435           1.0   1569   11:38:07
 7     -2933.721           1.0   1569   11:38:07
 8     -2933.720           1.0   1569   11:38:07

summary(modelz_3)$varcomp

                 component std.error   z.ratio bound %ch
year              8.029139 1.9920127  4.030666     P   0
vm(animal, ainv)  5.060775 1.7855255  2.834334     P   0
ide(animal)       8.412539 1.6494894  5.100087     P   0
units!units       7.805139 0.3331474 23.428484     P   0
units!R           1.000000        NA        NA     F   0

summary(modelw, coef = TRUE)$coef.fixed

             solution std error   z.ratio
(Intercept) 20.305073 0.2899515 70.029214
age_2        0.000000        NA        NA
age_3        2.577777 0.3355253  7.682811
age_4        4.247276 0.3309028 12.835418
age_5        6.094490 0.3375537 18.054872
age_6        3.132675 0.3371074  9.292811

wald.asreml(modelz_3, ssType = "conditional", denDF = "numeric")

ASReml Version 4.2 08/10/2024 11:38:07
          LogLik        Sigma2     DF     wall
 1     -2933.720           1.0   1569   11:38:07
 2     -2933.720           1.0   1569   11:38:07

$Wald
[0;34m
Wald tests for fixed effects.[0m
[0;34mResponse: laydate[0m

            Df denDF   F.inc   F.con Margin      Pr
(Intercept)  1  55.3 1894.00 1894.00        0.00000
age          4 845.2  152.70  132.90      A 0.00000
byear       33 466.5    0.77    0.77      A 0.81646

$stratumVariances
                         df  Variance     year vm(animal, ainv) ide(animal)
year               35.92378 144.92624 17.16741      -0.02687885 -0.06922989
vm(animal, ainv)  348.27527  50.82831  0.00000       3.50972263  3.00281025
ide(animal)        87.03390  34.64049  0.00000       0.00000000  3.18992331
units!units      1097.76705   7.80514  0.00000       0.00000000  0.00000000
                 units!units
year                       1
vm(animal, ainv)           1
ide(animal)                1
units!units                1

Wilson, A. J., D. Réale, M. N. Clements, M. M. Morrissey, E. Postma, C. A. Walling, L. E. B. Kruuk, et D. H. Nussey. 2010. An Ecologist’s Guide to the Animal Model. Journal of Animal Ecology 79:13‑26.